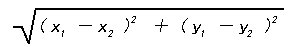|
10. BASICと愉快な算数
唐突にふざけたタイトルですが、寝ぼけている訳ではありません。
最近は、プログラムを作る人と使う人が明確に住み分けられてしまい、プログラミングで「遊ぶ人」が静かになったような気がしています。
まぁ、パソコンの歴史から見ても、誰もがBASICを使っていた(否、使わざるを得なかった)時代から、ソフトハウスとユーザーといった関係がより明確になり、それが今に至っている訳ですから、ある意味『餅は餅屋』というのが業界や市場の行き着く先なのかなとも思ってしまいます。
しかし、プログラム自体を楽しんでいる人も、また、ちょっと楽しんでみたい、と思っている人も少なくないんじゃないでしょうか?
本来、コンピュータを動かすために作るプログラムなので、その過程を目的とするのは、何か無駄なことをしているように思えますが、やってみれば意外と楽しかったりします。
今回は、そんな視点から、ちょっと変わったプログラミングを紹介してみましょう。
●タップと長方形
Palmデバイスといえば、スタイラスペンによる操作が1つの大きな特徴です。
手の大きなアメリカ人(偏見あり)が、こんな小さなスタイラスを持って「Oh!」とか言いつつ操作している姿を想像すると、微笑ましいものを感じますが、片手で持って操作することを考えれば、ペン操作は必然でしょう。もし、これがマウスのような間接的なデバイスだったら泣けてきます。
そんな標準のスタイラス、当然、NS Basicでもタップイベントを取得することが可能、むしろ、タップイベントが標準のイベントになっています。
例えば、画面の上の四角い領域で、タップのイベントを取得したい場合があるでしょう。
そういう場合に手っ取り早いのは、透明な四角のオブジェクト、Gadgetですね。
貼り付けたGadgetのイベントモジュールに、タップしたときの処理を記述すれば、目的は果たせますし、タップした位置もGetPenで取得できます。
当たり前のことですが「Gadgetをタップしなければイベントが発生しない」ということはとても重要です。
つまり、Gadgetを使えば、特定の長方形の範囲内をタップしたかどうか、簡単に知ることが出来るのです。
便利な一方で、長方形の範囲の中と外で処理を変えたい、という場合はちょっと厄介です。
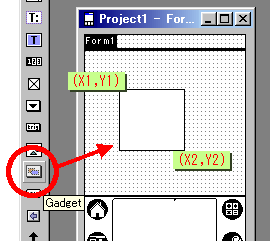
例えば、図のように、画面の中央の四角とその外で処理を変えようと、Gadgetを貼ってはみたものの、Form側のイベントに悩まされることになります。
つまり、Gadgetをタップしても、そのベントはFormのPenDown、FormのPenUp、Gadgetのタップの順に発生します。(※NS Basicのバージョン等によって変わる可能性はあります。)
要するに、最初にFormをタップした時点で、Gadget内外のチェックをしなければ正確な処理が出来ないということです。

もう少し進めて考えれば、そういう場合、Gadgetを貼る必要はないわけです。
優先されるForm上のイベントで、長方形のエリア内外のチェックをしたついでに、処理してしまえば済みますからね。
さて、タップした座標から、長方形の内外をチェックするには、If文を使った条件判定が一般的です。
|
If X > X1 and X < X2 and Y > Y1 and Y < Y2 Then
{長方形内の処理}
Else
{長方形外の処理}
End if
|
または、不等号をひっくり返してもほぼ同じ動作が得られます。
|
If X < X1 or X > X2 or Y < Y1 or Y > Y2 Then
{長方形外の処理}
Else
{長方形内の処理}
End if
|
正確には、"<"の逆は"≧"ですから、X < X1 じゃなくて、X <= X1 ですが、どちらにしろ、これをForm内のPenDownに相当する箇所に記述すれば目的は果たせます。
もちろん、プログラミング的にはここまでで十分なのですが、プログラミング自体を楽しむ場合、(多少理不尽な理由でも)ちょっとこだわってみます。
例えば、この条件判定を見て「AndやOrがたくさんあって、美しくない」とか(笑)
●算数すいすい
ここで
こんな関数を考えてみましょう。
って唐突に「関数」が登場したら、普通は退きますね。
でも、こいつはそんなに難しい関数じゃありません。
要するに、簡単なグラフを描くと、こんな感じになる2次関数です。
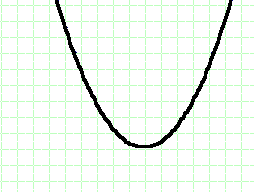
これが、x軸と接点があるか交われば、方程式f(x)=0の解を持っていることになります。
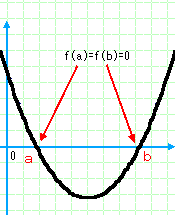
詳しいことはともかく、重要なのは、次の図のような「状態」が存在することです。
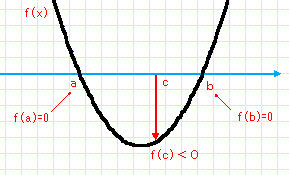
f(c)<0となる場合、これは、a<bであれば、必ずa<c<bという関係が成り立ちます。
授業中は、この「状態」に様々な説明がついてきて、頭の中が混乱したかもしれませんが、少なくとも図で見れば、この関係は直感的に理解できるような気がしませんか?
つまり、f(x)=(x-a)(x-b)の、xに適当な値cを代入した時、
- f(c)<0ならば、a<c<b
- f(c)>0ならば、c<a、または、b<c
という関係が成り立ちます。
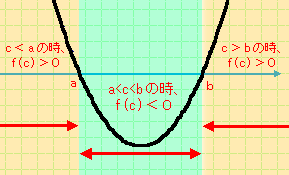
賢明な方なら、ここで気づきましたね。
この関数は、ある数値が特定の範囲内にあるかないかを判別するのに使えます。
先ほどの長方形の座標に置き換えて考えれば、
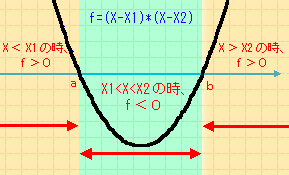
|
f(x)=(X-X1)(X-X2)
g(y)=(Y-Y1)(Y-Y2)
|
もちろん、縦方向と横方向の2つの値が必要ですから、2つの関数が必要です。
プログラムらしくしてみると、
|
f=(X-X1)*(X-X2)
g=(Y-Y1)*(Y-Y2)
If f>0 and g>0 Then
{長方形外の処理}
Else
{長方形内の処理}
End if
|
行が増えたものの、条件判定は「スッキリ」と、AndやOrが並んでいなくて美しい気がしますね。たぶん…
一応、こういう事をすると実行速度が極端に遅くなるじゃないか、という疑問にフォローしておきますと、見た目の数式の複雑さと実行速度は深い関係にありません。
例えば、
という数式は、
|
f= X * X - X1 * X - X2 * X + X1 * X2
|
と数式を展開してカッコを外すことが出来ます。
一見すると、後者の方は、カッコがなくなったことで数式が「ストレート」になり、前者より速いんじゃないかと思うかもしれません。しかし、実際、ランタイムの性能というか仕様によるので、どちらが速いと決めることが出来ません。
確かに、カッコがなければ数式が単純になって計算は速くなりそうですが、その分、掛け算の処理が増えることになります。
通常、掛け算、割り算はCPUに対して思ったよりストレスがかかります、もしかしたら展開前の方が速いかも知れません。
要するに、実行速度は人間の見た目ではなく、そのランタイムなりマシンなりが「得意な」数式ほど高速に処理ができるということです。
●使えりゃ勝ち(価値)
関数だの何だの言われると、どうも構えてしまいがちですが、先ほどの2次関数f(x)など、使ってみれば意外に便利です。
ところで、2次関数だとグラフの形が分かりやすいため、頭の中でイメージしやすいですが、これが高次の関数になるとどうでしょうか?
例えば、
|
fn(x)=(x-a1)(x-a2)(x-a3)…(x-an)
|
のような関数。勘弁してくれ、という声が聞こえてきそうですが、確かにグラフをイメージするのはちょっと困難です。
そんな厄介モノですが(理解できなくても)使ってみれば意外と便利です。
簡単な算数ですが、次のような掛け算の性質があります。
|
★a×b×c×d=0ならば、
少なくとも、aかbかcかdか、どれかは1つは0である
|
まぁ、0に何を掛けても0ということなのですが、これを、先の高次関数に当てはめてみれば、
|
fn(x)=(x-a1)(x-a2)(x-a3)…(x-an)=0
が成り立つ場合、
x=a1,x=a2,x=a3,... ,x=an
このうち、少なくとも1つは成立する
|
これを使えば、1つの数式で複数の値との比較が可能になります。
例えば、ゲームなどの複数の敵や弾などとの衝突判定に使えそうですが、For〜Nextでループさせるほどでもないし、IfにAndやOrを並べるのも「美しくない」という場合に使うと効果的です。
意外と使える数式の性質、足し算なら、次の性質をよく使います。
(実際は2変数で使うことに、あまり意味はありませんので、もう少し複雑になりますが…)
|
★a≧0,b≧0(または、a≦0、b≦0)の時
a+b=0なら、a=b=0
|
もちろん、無理に数式を使う必要はありませんが、NS Basicのように不完全なAnd、Orしか提供されていない言語では重宝するでしょう。
●ここにも算数
さて、見た目の美しさで満足(自己満足)した長方形の次は「円」に挑戦してみましょう。
円の中をタップしたかどうかを知るようなオブジェクトは用意されていませんので、こちらこそ、何とかしなければなりませんが、やっぱりここでも算数は有用です。
いきなり数式でスミマセンが、半径Rの円は、次の「式」で表されます。
詳しく状況説明をするならば、この式は、次のような円を表しています。
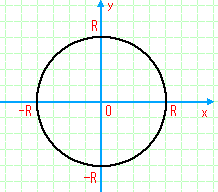
この式は、中心(0,0)からの距離が一定の値(=R)である、点(X,Y)の集まりを表した「関係式」といえます。
ちなみに、2点(X1,Y1)、(X2,Y2)の間の距離は、
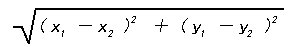
です。(さすがに、この式の詳細までは説明しませんが、三平方の定理などを使って考えると面白いですよ。)
言い換えるなら、ある位置から一定の距離にある点は、全て円周の上に存在しているわけです。
では、ここでPalmの画面の1点(79,79)を中心として考えてみましょう。
タップした位置(X,Y)が、中心から例えば50ピクセルの距離内にあるかどうかを知りたい場合、
であればよい訳です。
図にすると分かりやすいですが、これで、円形のエリア内のタップ判別が出来るようになりました。
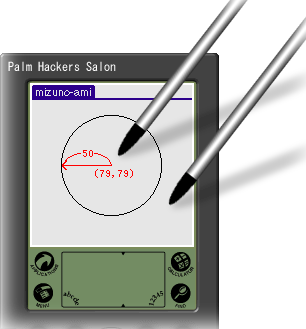
一方、中心からの距離は、
|
R=Sqrt((79-X)^2+(79-Y)^2)
|
で計算できますが、これは円の半径ですね。(※Sqrt()の利用には、MathLibが必要なのが痛いですが…)
これを利用して、次のようなゲームが作れます。
|
Dim X as Integer
Dim Y as Integer
Dim R as Single
Dim Sc as Integer
If GetEventType()=NsbPendown Then
GetPen X,Y,NsbPenDown
R=Sqrt((79-X)^2+(79-Y)^2)
Sc=100-5*Int(R/5)
MsgBox "得点:"+Str(Sc)+"点"
End If
|
プログラム自体は簡単ですが、これを実際のゲームにしようと思うとかなり難しいです。
なぜなら、単純に画面をタップしても面白くも何ともありません。実際に、距離をおいたところから、ダーツなり、エアガンなりで実射しなければ…
ということで、実際にゲームを試すのは、強靭なPalmをお持ちの方、または、犠牲を払っても試してみたい、という方にお譲りします。
※重要な注意:勿論、mizuno-amiもPalm Hackers Salonも、一切の責任は負いません。試すことによる如何なる不具合や不利益も、全て自己責任でお願いします。
さて、一部、拙作Basic BASICと重なる部分もありますが、算数とプログラミングの意外と面白い組み合わせを紹介する意味で、あえて掲載させていただきました。
本来、プログラミングの講座は、プログラムをより効率的に開発する手法を求めるべきでしょうが、プログラミング自体を楽しんでもバチは当らないでしょう。
むしろ、人間の言語に近い(ようにも思えませんが)という位置付けのBASIC、こんな具合に「対話」をしながら楽しむのも「有り」じゃないでしょうか。
ひとまず、本稿を「学生の頃聞いていれば〜、数学好きになったかも」と言う声など期待しつつ、今回のお話を終わらせていただきます。
|